
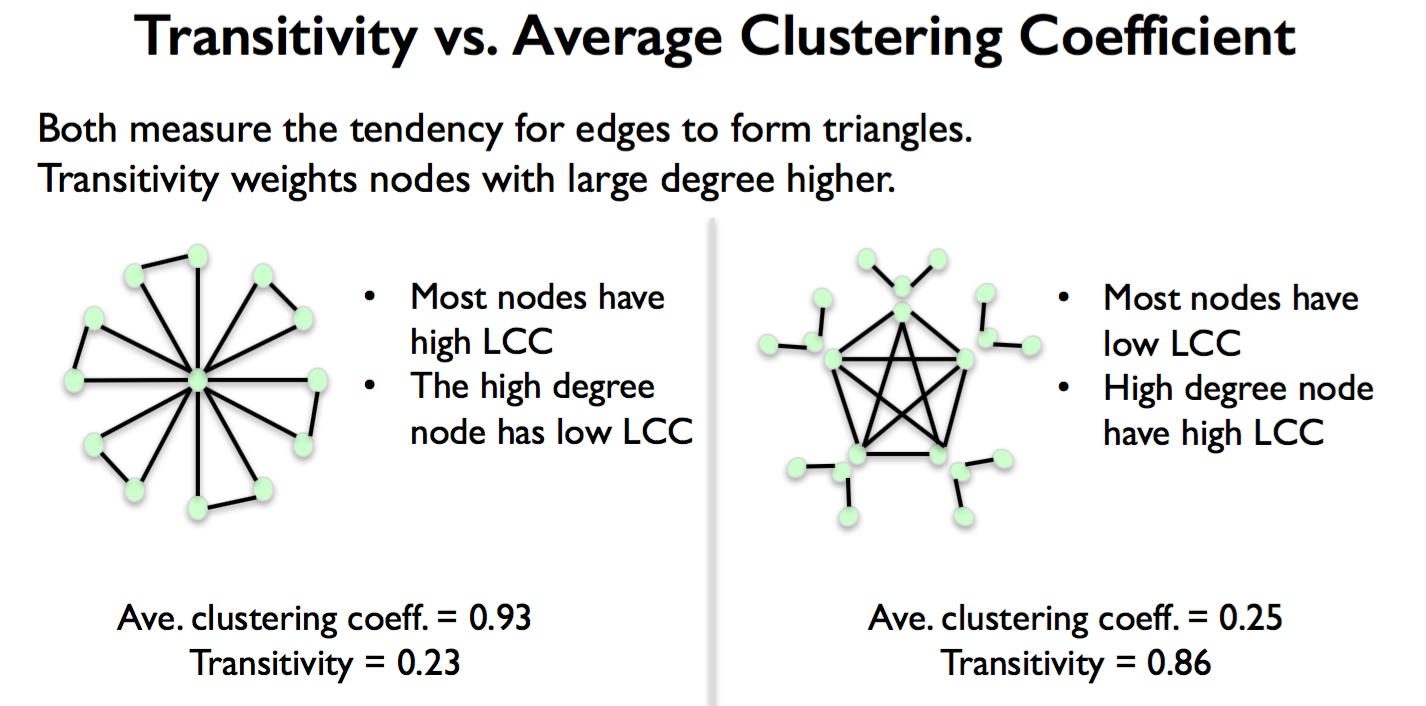
In its usual definition for binary networks, the graph transitivity corresponds to the relative frequency of closed and open triplets ( Newman, Watts, & Strogatz, 2002 see also Watts & Strogatz (1998) and Barrat et al. The transitivity influences the occurrence of indirect interactions (when B and C are not connected) as well as the expected shortest path length influencing the circulation of pathogens and information.


The graph transitivity answers the question: when A is separately connected to B and to C, what is the probability that B and C are also connected. Here I focus on the graph transitivity ( Newman et al., 2002). In that context, it seems useful to develop network summary metrics that account for edge weights ( Barrat et al., 2004), instead of dichotomizing the network or to scale the timeframe down until interactions can be considered binary. And even if the instant interactions indeed have a binary outcome, the consequences usually accumulate over several interactions, e.g., the fitness benefits of long-lasting bonds ( Silk et al., 2009), and the hierarchy emerging from successive agonistic interactions ( Franz et al., 2015). Instead, the connections between individuals vary in strength or valence. Social interactions between individuals are rarely binary. In the barnacle goose Branta leucopsis, in an experiment designed to test the long-term effect of the goslings’ social environment, the new metrics uncovered an excess of weak triplets closed by strong links in males compared to females, and consistent with the triadic process underlying goose dominance relationships. In the rhesus macaque Macaca mulatta, a species in which kin relationships strongly predict social relationships, the new metrics revealed striking similarities in the configuration of grooming networks in captive and free-ranging groups, but only as long as the matrilines were preserved. I illustrate the biological relevance of that information with two reanalyses of animal contact networks. I score the weighted transitivity according to the similarity between the weights of the three possible links in each triad. When the connections vary in strength, focusing on whether connections exist or not can be reductive. The graph transitivity measures the probability that adjacent vertices in a network are interconnected, thus revealing the existence of tightly connected neighborhoods playing a role in information and pathogen circulation.


 0 kommentar(er)
0 kommentar(er)
